AtCoder Beginner Contest 087 - takahiro_itazuriの公倍数的ブログ

はじめに
A - Buying Sweets
- 自分の解答
- 改善点
B - Coins
- 自分の解答
- 改善点
C - Candies
- 改善点
D - People on a Line
- 解答
総括

はじめに

AtCoderのBeginner Contest 087の解説と勉強です。
問題はこちらを参照してください。

A - Buying Sweets

int同士の割り算の性質を利用すると簡単です。

自分の解答

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<stack>
#include<queue>
#include<map>
#include<tuple>
#include<algorithm>
#include<numeric>
#include<math.h>

#define REPS(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)

using namespace std;

using ll = long long;
using pii = pair<int, int>;
using vi = vector<int>;

const int mod = 1e9 + 7;
const long double pi = 3.141592653589793238462643383279502884197;
const long double eps = 1e-7;

int main() {
  int X, A, B;
  scanf("%d", &X);
  scanf("%d", &A);
  scanf("%d", &B);

  X -= A;
  int n = X / B;
  X -= n * B;

  printf("%d\n", X);

  return 0;
}

改善点

特になし。

B - Coins

「入力$X$が$50$の倍数である」という制約があるので、最初にすべて$50$円玉に変換してしまいます。
あとは全探索を行い、枚数の制約を満たしているかを判定します。全探索の仕方としては、$50$円玉$2$枚を$100$円玉$1$枚に変えていき、そこから取りうる$500$円玉の枚数をすべて探索することで可能になります。要するに$50$円玉の枚数を固定した時に取りうる$100$円玉と$500$円玉の組み合わせを考えるということです。

自分の解答

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<stack>
#include<queue>
#include<map>
#include<tuple>
#include<algorithm>
#include<numeric>
#include<math.h>

#define REPS(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)

using namespace std;

using ll = long long;
using pii = pair<int, int>;
using vi = vector<int>;

const int mod = 1e9 + 7;
const long double pi = 3.141592653589793238462643383279502884197;
const long double eps = 1e-7;

int A, B, C, X;
int a = 0, b = 0, c = 0;
int num = 0;

int main() {
  scanf("%d", &A);
  scanf("%d", &B);
  scanf("%d", &C);
  scanf("%d", &X);


  for (int c = X / 50; c >= 0; c -= 2, b += 1) {
    for (int _a = a, _b = b; _b >= 0; _b -= 5, _a += 1) {
      if (_a <= A && _b <= B && c <= C) num++;
    }
  }

  printf("%d\n", num);

  return 0;
}

改善点

特になし。

C - Candies

通常であれば、動的計画法で解きます。
ただし、今回は$2$行しかないので、一度下に進むと右に進むしかないという制約から、非常に簡単に解くことができます。
上の行は左側から、下の行は右側から累積和を取っておくことで、取ることのできるアメの合計を用意に計算できます。
こうすることによって、$O(N)$で解くことができます。

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<stack>
#include<queue>
#include<map>
#include<tuple>
#include<algorithm>
#include<numeric>
#include<math.h>

#define REPS(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)

using namespace std;

using ll = long long;
using pii = pair<int, int>;
using vi = vector<int>;

const int mod = 1e9 + 7;
const long double pi = 3.141592653589793238462643383279502884197;
const long double eps = 1e-7;

int main() {
  int N;
  cin >> N;

  int A[2][101];
  REP(i, 2) {
    REP(j, N) {
      cin >> A[i][j];
    }
    A[i][N] = 0;
  }

  // 累積和を取る
  for (int i = 1; i < N; i++) {
    A[0][i] += A[0][i - 1];
  }

  for (int i = N - 2; i >= 0; i--) {
    A[1][i] += A[1][i + 1];
  }

  int max = 0;

  REP(i, N) {
    if (max < A[0][i] + A[1][i]) {
      max = A[0][i] + A[1][i];
    }
  }

  cout << max << endl;
  return 0;
}

改善点

特になし。

D - People on a Line

配点は400点ですが、かなり難しかったです。
基本的には、２人の間の条件がたくさん与えられるため、グラフ構造を取ると良いんです。さらにその条件には、左と右という区別がができるため、有向グラフを使用するとよりよいです。

まず条件$0 \leq D_i \leq 10^4$と$0 \leq x_i \leq 10^9$と$1 \leq N \leq 10^5$から、全ての人が最大限に離れていた（$10^5$人が$10^4$ずつ離れて並んでいる）としても、はみ出てしまうことはないので、この判定は必要ありません。

判定の一つ目としては、一番左の人から条件に沿って右の人を探索していき、他の経路と矛盾が発生した場合がダメであるという点です。この探索には深さ優先探索を行います。ここでいう深さは条件として左に人がいる必要がない人たちからの探索回数ということになります。これを判定するために「その人より左に人がいるべきかどうか」の真偽値を持つ配列（デフォルトはfalse）を用意します。各条件に対して、右となる人たちにはtrueを割り当てます。すると、何も条件がない人であるか左に人がいる必要がない人がfalseの値を持っています。その人から探索を行います。

判定の二つ目としては完全なループ（下図）ができてはいけない点です。
完全なループの例えとしては、「$A$は$B$より右、$B$は$C$より右、$C$は$A$より右」とはならないということです。

f:id:takahiro_itazuri:20180129140025p:plain:w300

実は既にこの対策がされています。先程の「その人より左に人がいるべきかどうか」の真偽値を持つ配列において、完全なループができた場合には、すべての人がtrueになるため、探索が行われません。逆に完全なループ外の人たちは必ず１回ずつ探索が行われます。なぜならば、2回目であった場合は、探索ではなく矛盾が発生しているかを判定するプログラムが回るためです。

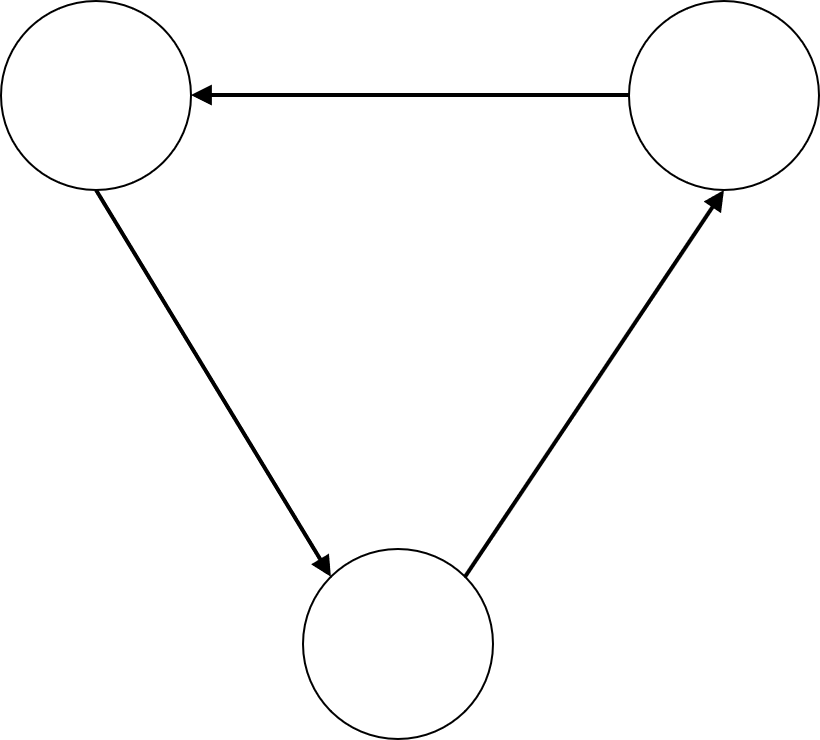
一方、完全なループでないループ（下図）が存在する場合は、一つ目の判定の際に、矛盾が発見されます。

f:id:takahiro_itazuri:20180129140229p:plain:w300

したがって、完全なループが含まれているかどうかを判定するためには、何回探索が行われたかを数え上げ、ノードの数と一致するかを判定することで問題を解くことができます。

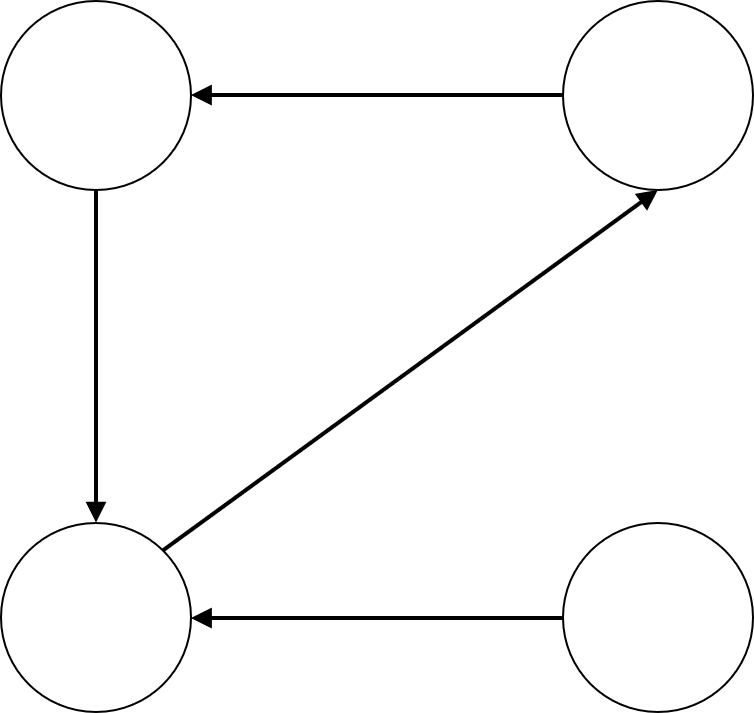
解答

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<stack>
#include<queue>
#include<map>
#include<tuple>
#include<algorithm>
#include<numeric>
#include<math.h>

#define REPS(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)
#define print(x) cout << #x << " = " << x << endl;

using namespace std;

using ll = long long;
using pii = pair<int, int>;
using vi = vector<int>;

const int mod = 1e9 + 7;
const long double pi = acos(-1);
const long double eps = 1e-7;


const int MAX = 100001;

int n, m;
int l, r, d;
int numNode;		/	/ 使用した条件の数え上げ
vector<pii> terms[MAX];	// 条件（first: エッジの先のインデックス、second：距離）
bool bHasLeft[MAX];		// 左に人がいるかどうか
bool bSearched[MAX];	// 探索をすでにしているかどうか
int dis[MAX];			// 距離を保存
bool bWrong;			// 矛盾が発生しているかどうか

// 深さ優先探索
void dfs(int p) {
  bSearched[p] = 1;
  numNode++;

  // インデックスpのノードにおける条件すべてをループ
  for (pii term : terms[p]) {
    if (!bSearched[term.first]) {	// エッジの先がまだ探索されていない場合
      dis[term.first] = dis[p] + term.second;	// 距離を保存
      dfs(term.first);	// 次のエッジを探索
    }
    else {	// エッジの先がすでに探索済みである場合
      if (dis[p] + term.second != dis[term.first]) {	// 既に探索した道のりと現在辿ってきた道のりが異なる場合
        bWrong = true;
        return;
      }
    }
  }
}

int main() {
  scanf("%d %d", &n, &m);

  for (int i = 0; i < m; i++) {
    scanf("%d %d %d", &l, &r, &d);

    terms[l].push_back(pii({ r, d }));
    bHasLeft[r] = true;
  }

  for (int i = 1; i <= n; i++) {
    // 左に人がいる時はスキップ
    if (bHasLeft[i]) continue;

    // 一番右になりえる要素から探索スタート
    dfs(i);
  }

  if (bWrong || numNode < n) printf("No\n");
  else printf("Yes\n");

  return 0;
}

総括

いつも問題Dは難しくて悩まされます。まだまだですね。
今回のようなグラフをイメージする問題はあまり取り組んだことがなかったので、非常にいい機会でした。
それではまた次回。