【就プロ】深さ優先探索

はじめに

深さ優先探索（depth-first search, DFS）は簡単に述べると「行けるところまで進んでそれ以上進めなくなった場合、他に探索が行えるようになるまで戻るという方法」です。

以下の画像はWikipediaより添付させていただきました画像です。

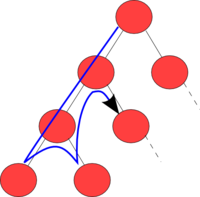
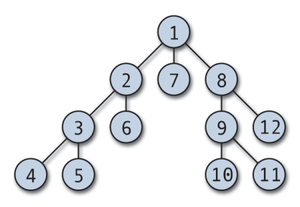
深さ優先探索に対して幅優先探索という探索アルゴリズムもあります。
幅優先探索については以下の記事で解説しています。

takahiro-itazuri.hatenadiary.jp

深さ優先探索はツリー構造やグラフの探索を行うためのアルゴリズムです。

グラフ構造の探索においては
時間計算量は$O(\|E\|)$
空間計算量は$O(\|V\|)$
となります。

深さ優先探索を実装する方法を今回は２つご紹介します。

そのためにまず問題定義をしておきます。

問題設定

問題文

$N \times N$の碁盤目状の道がある時、$(x,y)=(1,1)$から$(x,y)=(N,N)$に行くための最短経路の数を数えろ。

入力

碁盤の目の数$N$

N

出力

最短経路の総数

アルゴリズムと実装

再帰関数

考えるべきことは以下の通りです。

• 状態を引数にした再帰関数を使用する
• 次の状態への呼び出しを行う

アルゴリズムは以下のようになります。

1. 状態を初期化
2. 関数内で深さを優先するように再帰関数を呼ぶ

再帰関数を利用する理由としては、再帰関数なので呼び出し元に戻ってくる性質があるからです。
再帰関数を用いる場合は、深くなりすぎると「スタックオーバーフロー」が起こって実行時エラーになることがあります。
再帰関数については以下の記事で解説しています。

takahiro-itazuri.hatenadiary.jp

C++

#include<iostream>

int count = 0;
int N;

void DFS(int x, int y) {
    // 終了条件
    if (x == N && y == N) {
	count++;
	return;
    }

    if (y < N) DFS(x, y + 1);

    if (x < N) DFS(x + 1, y);
}

int main(int argc, char* argv[]) {
    std::cout << ">> ";
    std::cin >> N;

    DFS(1, 1, 1);

    std::cout << count << std::endl;
    system("pause");
    return 0;
}

実行例
以下のように深い順に探索されていることがわかります。

>> 3
6

スタック

考えるべきことは以下の通りです。

• スタックで探索待ちしている状態を管理

アルゴリズムは以下のようになる

1. スタックを初期化する
2. スタックの一番後ろにある要素をバッファに格納してpopする
3. バッファの要素から探索を行い、優先順とは逆順にスタックの後ろに追加する
4. スタックが空になるまで、2~3を繰り返す

スタックの場合は、再帰関数のように呼ばれる度に必要な変数を確保する必要がないため、スタックオーバーフローは発生しにくいです。

C++

#include<iostream>
#include<vector>

int N;
int count = 0;

struct pos {
    int x;
    int y;
};

class Stack {
public:
    Stack();
    ~Stack();
    void push(pos p);
    pos pop();
    void search(pos p);
    void show();
    bool isEmpty();
private:
    std::vector<pos> stack;
};

Stack::Stack() {
    stack.push_back({ 1, 1 });
}

Stack::~Stack() {}

void Stack::push(pos p) {
    stack.push_back(p);
}

pos Stack::pop() {
    pos p = stack[stack.size() - 1];
    stack.pop_back();

    if (p.x == N && p.y == N) count++;

    return p;
}

void Stack::show() {
    int length = stack.size();
    for (int i = 0; i < length; ++i) {
	if (i == length - 1) std::cout << "[" << stack[i].x << ", " << stack[i].y << "]" << std::endl;
	else std::cout << "[" << stack[i].x << ", " << stack[i].y << "] -> ";
    }
}

bool Stack::isEmpty() {
    if (stack.size() == 0) return true;
    else return false;
}

void Stack::search(pos p) {
    if (p.x < N) stack.push_back({ p.x + 1, p.y });
    if (p.y < N) stack.push_back({ p.x, p.y + 1 });
}

int main(int argc, char* argv[]) {
    std::cout << ">> ";
    std::cin >> N;

    Stack s;

    while (!s.isEmpty()) {
	pos p = s.pop();
	s.search(p);
    }

    std::cout << count << std::endl;

    system("pause");
    return 0;
}

実行結果

>> 3
6